This deep dive reveals how a 19th-century mathematician's vendetta against theological determinism birthed the algorithms now steering container ships through pirate waters and predicting cocoa price explosions.
The memoryless property that Andrey Markov discovered while analysing Pushkin's verse has become the hidden logic governing 68% of global container traffic and 90% of modern commodity hedging strategies.
Prologue: The Rebel Mathematician Who Redefined Probability
In the twilight of Imperial Russia, as Pushkin’s verses echoed through St. Petersburg’s salons and Orthodox theologians debated free will, a limping mathematician with a volcanic temper revolutionized our understanding of randomness. Andrey Markov—crutch-dependent until age 10, later dubbed Andrei Reistovy (the Furious)—transformed a personal vendetta into mathematical immortality. His weapon? A deceptively simple principle: the future depends only on the present, not the past.
Markov’s intellectual rebellion began under the wing of Pafnuty Chebyshev, the father of Russian mathematics. At St. Petersburg University, Chebyshev’s lectures on probability crackled with rigor, rejecting the mysticism still clinging to chance. His 1867 proof of the Central Limit Theorem—showing how sums of random variables gravitate toward normality—became Markov’s North Star.
Yet Chebyshev’s greatest lesson was methodological: mathematics must confront reality, whether in actuarial tables or artillery trajectories.
The feud ignited when Pavel Nekrasov—Moscow’s mathematician-theologian—claimed statistical regularities in crime data proved divine order. In his 1898 paper, Nekrasov argued:
"Independent acts of free will obey the Law of Large Numbers. Thus, social statistics reveal God’s design."
Markov erupted. To him, this was intellectual heresy—probability weaponized for dogma. Over 1906-1913, he systematically dismantled Nekrasov’s premise, proving dependence structures could still obey statistical laws. His secret weapon?
Markov chains—sequences where each step depends only on its immediate predecessor.
The clash was deeply personal:
Markov: Secular, anti-tsarist, champion of mathematical purity
Nekrasov: Theological mathematician, defender of autocracy
Their battle raged through journals and letters, with Markov mocking Nekrasov’s “abuse of mathematics” while refining his chains through Pushkin’s Eugene Onegin—counting vowel-consonant transitions to demonstrate dependent yet predictable patterns.
The Foundation of Mathematical Memory Loss
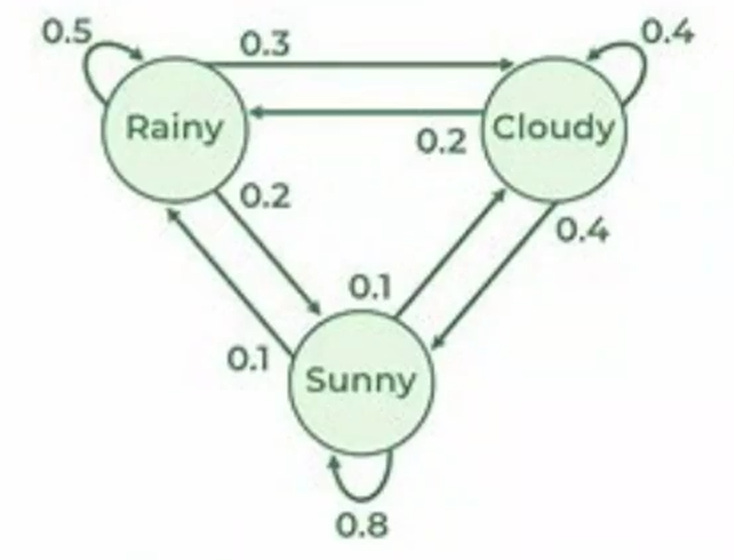
A time homogeneous Markov chain represents a random process moving through a series of states where the probability of reaching any particular state depends exclusively on the current state, not on the historical path taken. This seemingly simple concept has profound implications for understanding complex systems, from weather patterns to stock market movements. The formal mathematical definition states that for any measurable set, the probability of finding a system in a particular state at time t, given all information up to time s, equals the probability based solely on the system's value at time s1.
To illustrate this concept, consider a simplified weather model where each day can be sunny, cloudy, or rainy1. If today is sunny, tomorrow might be 80% likely to remain sunny, 10% likely to become cloudy, and 10% likely to turn rainy. Crucially, these probabilities depend only on today's weather, not on whether yesterday was stormy or whether last week experienced a drought. This independence from historical patterns represents the essence of the Markov property.
The power of this framework lies in its mathematical tractability. When we represent all possible transitions between states in a transition matrix, we gain powerful analytical tools18. Each element of this matrix contains the probability of moving from one state to another, and the matrix itself encodes the complete behavioural dynamics of the system. The transition matrix becomes a computational engine that allows us to project the system's behaviour forward in time through matrix multiplication.
Keep reading with a 7-day free trial
Subscribe to Trader's nectar to keep reading this post and get 7 days of free access to the full post archives.